Plasmamr_task_types

Plasma MapReduce: The task types

This page tries to give some background information on how PlasmaMR decomposes a job into tasks, and which task types are used. In this respect PlasmaMR is very different from other map/reduce implementations, as it employs fine-grained job decomposition. This means that all processing steps reading or writing files are considered as a task, and not only those steps that drive the user-specified map and reduce functions. This approach raises interesting questions about what the best decomposition is, as we'll see.

As all data files reside in PlasmaFS (and there are no files in the local filesystem), every task can be principially run on every node. If the PlasmaFS files accessed by the task are stored on the same node, the accesses are very fast (even shared memory is used to speed this data path up). If the files are stored on a different node, PlasmaFS is responsible for making the files available via network. On the one hand this raises the transport costs, but on the other hand more CPU cores can be used (or more flexibly used) to execute the tasks. Of course, there are lots of ways of assigning tasks to nodes, and some are better than others. We discuss this in more detail below.

The input data

Before the job is decomposed, the input data is analyzed. The input data can be given as one or several PlasmaFS files, with or without block replication. The data is now cut into pieces, so that

• each piece consists of data blocks that are stored only on one node (at least to a high likelihood)
• the physical contiguity of these data blocks is high, i.e they are mostly stored adjacent to each other on the disk (remember that PlasmaFS has full control over this aspect)
• the number of the pieces is a small multiple of the minimum that is needed to keep the cluster busy when the pieces are processed in parallel

Example.

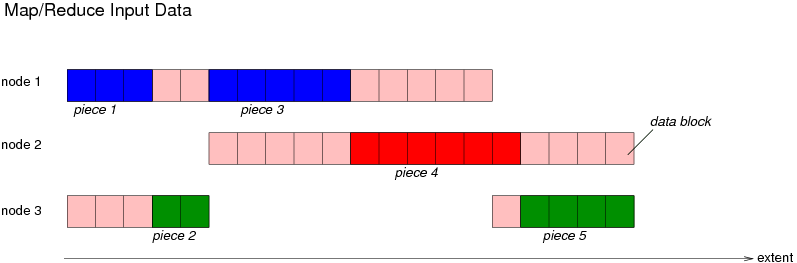
This picture show a file with a replication factor of two, i.e. each data block is stored on two nodes. The system splits the file up into five pieces (red, blue and green block ranges). Because each block is available on two nodes, it is possible to select each block from two nodes. It is now tried to make the block ranges as large as possible while creating enough pieces in total.

Formally, each piece is described as a list of block ranges coming from input files (see types Mapred_tasks.file and Mapred_tasks.file_fragment). In the following, we refer to this input as "pieces of input data", and D be the number of pieces.

The task types

Right now, the following types are implemented:

• Map tasks read a piece of input data, apply the user-defined map function to the input, and write the results to new intermediate files. Each Map task creates at least one file but it will create more than one if the amount of data exceeds the sort limit. As these intermediate files are further processed by Sort tasks it is possible to apply an optimization here. Sorting is easier to do if it is known in advance how much data is to be sorted. By keeping the size of the intermediate files below the sort limit, the Sort tasks can be written so that all sorting occurs in RAM.
• Sort tasks read the intermediate files created by Map, and they sort these files so that records with equal keys are grouped together. The result is written into new intermediate files (of equal size than the sort inputs).

This example illustrates these two types:

Here, we found three input pieces, and each piece is mapped to a map output. For the second map operation we got more output than sort_limit allows, and hence two map output files are created. So the Map round of tasks created four output files in total, and each of these files is sorted.

After sorting, the data is available in this form: There are N sorted files where each file stems from one input piece. There can be more sorted files than input pieces, i.e. N can be larger than D. The remaining algorithm needs now to merge all these sorted files, and it has to split the data into P partitions at the same time (remember that the keys of the records are partitioned into P sets). We call these sets "partition 0", ..., "partition P-1".

Merging and partitioning is done by applying the following type of task several times:

• Shuffle tasks read a variable number of input files, and merge these files so that the sort criterion remains intact. Furthermore, the merged data is written to a variable number of output files, so that each file gets only records falling into a certain range of partitions. There are limits for the number of input and output files, called merge_limit and split_limit.

This picture merges the inputs and splits them into s output files:

For the inputs we already know that the keys of the inputs fall into a range of r partitions. The outputs are now further split in a way so that each of the s files contains the records from partition ranges that are s times smaller.

This task type allows a lot of constructions. For example, one could first merge all the N sort output files to a single file, and then split this file into P partitions, i.e. we first run Shuffle tasks where only merging happens, and then Shuffle tasks with only splitting. Another construction would do the converse: First split the N sort outputs further up into N*P smaller files, and then merge these files into P partitions. However, what PlasmaMR really does is a mixture of both approaches: In several rounds of data processing, Shuffle tasks are run that both merge and split to some extent. This is seen as best method because it allows a lot of parallel processing while not creating too many intermediate files. It is explained in more detail below.

• Reduce tasks are Shuffle tasks where the is_reduce flag is set. This enables that the user-defined reduce function is run. Reduce tasks are only created in the final step of shuffling, i.e. when the output files are the final output files of map/reduce. Also, it is (for now) required that no splitting occurs.

There is also now a fifth type of task: enhanced map tasks, or Emap tasks (since Plasma 0.4):

• Emap tasks actually do a combination of Map, Sort and Shuffle. The existence of this type is justified because it can be implemented without intermediate files. An Emap task first runs the user-specified map function on a piece of input data. The result is split into several output sets (kept in RAM buffers). Whenever the sets reach a size comparable to sort_limit, the sets are sorted in RAM, and finally written to output files, split by partition ranges.

This diagram shows how Emap tasks could be composed of existing Map, Sort, and Shuffle tasks. Note that the current implementation is different in so far first the data is split into partitions, and then the pre-partitioned data is sorted.

The scheduler only creates Emap tasks when it is configured to do so. The number of output sets is a parameter (Mapred_def.mapred_job_config.enhanced_mapping). Experimentation showed so far that Emap is not always an improvement, in particular because a higher number of intermediate files are created, resulting in higher data fragmentation, and more work for merging data.

Constructing execution graphs

PlasmaMR represents execution graphs explicitly (in Mapred_sched): The execution order of the tasks is not hard-coded in a fixed algorithm, but the order of steps is expressed as a graph where vertexes represent either data or tasks, and the edges represent the data flow (and implicitly the execution order). This has a number of advantages:

• more complicated execution flows are possible (e.g. more parallelism opportunities can be exploited)
• more modular design - the graph construction can be separated from graph execution
• the graph can be annotated so that better execution becomes possible (e.g. on which nodes which files are stored)
• the graph can be constructed without executing it (option -simulate of the exec_job command) - easing research on graph construction
• the graph can be visualized (option -dump-svg of exec_job)

The construction algorithm is generally an iterative process that progresses while the already constructed part of the graph is being executed. It is not possible to create the graph in one go because there are some aspects that depend on the outcome of already executed tasks. In particular, the Map (or Emap) tasks can emit a variable number of output files, and the number influences the layout of the graph. We could now wait until the execution has reached the point so that the number of all these files is known, and first continue the graph construction at this point. However, this would mean that the parallelism of execution was greatly reduced because the number of executable tasks decreases to 1 while approaching this point in the construction process.

As a better alternative, the graph is extended so far possible whenever an executed Map or Emap task has produced outputs. This means that dependent tasks are added as soon as possible, and generally more tasks are considered as executable in the construction/execution process.

Another advantage of the iterative construction is that even the locality of files (i.e. on which nodes files are really stored) can sometimes be used to optimize the graph.

Execution graphs with Map, Sort, and Shuffle

The following diagam shows an execution graph for D=N=3 and for P=4 partitions:

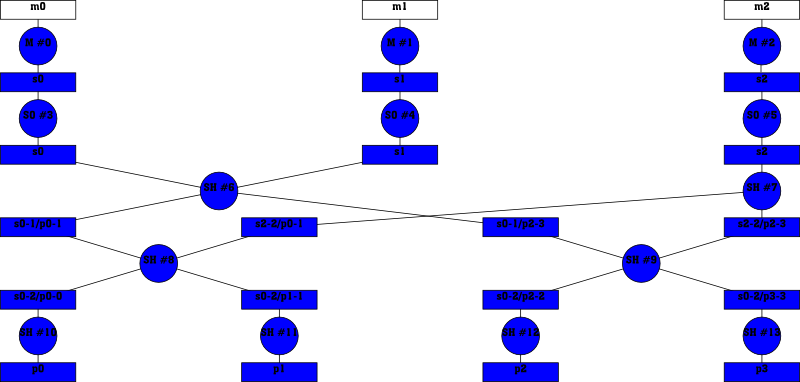
Notation:

• M: Map tasks
• SO: Sort tasks
• SH: Shuffle tasks
• #n: the task ID (assigned at execution time)
• mn: input piece to map number n
• sn: map or sort output number n
• sm-n/pu-v: this file contains data from sm to sn falling into the partitions u to v
• pu: output partition u

The last four shuffle tasks #10 to #13 are also Reduce tasks (i.e. run the user-defined reduce function).

The graph can be analyzed in the following ways:

• How much parallelism is possible at execution time?
• How often needs the data to travel over the network?
• How big are the smallest data items? Are random disk seeks avoided?

Note that the above diagram has been produced with the -dump-svg switch of exec_job. When generating diagrams for larger jobs, the following observations are easier to make.

Roughly, the graph is executed top to bottom. The possible parallelism is limited by the number of tasks in the same row. For instance, this diagram has a row with only SH #6 and SH #7, so at this point of execution only these two tasks can run at the same time.

Another observation is that the locality of the data increases from top to bottom. For example, once SH #6 and SH #7 are done, the whole data set is split into two independent halves. If each half was executed on its own machine, there was no need for a task on one machine to get the output of a task that ran on the other machine. Generally, once the number of partitions exceeds the number of nodes, there is no need anymore to access data over the network.

In each round of data processing (as indicated by the "rows" of the diagram) a certain number of files is merged, and the data is again split into a certain number of files. If now D and P are roughly in the same order of magnitude, the sizes of the files will not dramatically change from round to round. Especially, very small files are avoided, and random disk seeks are never required to gather up small fragments from the disk.

Execution graphs with Emap and Shuffle

Assigning tasks to nodes

This web site is published by Informatikbüro Gerd Stolpmann